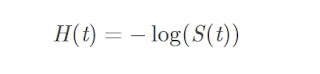Cox Proportional hazards model, what is it for?

 In suivival analysis, S(t)=p(T>t) denote the probablity an event survived time t, called survival probablity.

Kaplan-Meier survival estimate, it is a non-parametric method to estitmate the survival probability based on the survival times. 

Log-Rank test , after KM, it is not easy to do the test still. Then we use log-rank test to compare several survival curves. 

hazard probability. 

cummulative hazard

from survival equation S(t), we can get cummulative hazard. 

Cox Proportional hazards model

One R example

covariates <- c("age", "sex", "ph.karno", "ph.ecog", "wt.loss") univ_formulas <- sapply(covariates, function(x) as.formula(paste('Surv(time, status)~', x))) univ_models <- lapply( univ_formulas, function(x){coxph(x, data = lung)}) # Extract data univ_results <- lapply(univ_models, function(x){ x <- summary(x) p.value<-signif(x$wald["pvalue"], digits=2) wald.test<-signif(x$wald["test"], digits=2) beta<-signif(x$coef[1], digits=2);#coeficient beta HR <-signif(x$coef[2], digits=2);#exp(beta) HR.confint.lower <- signif(x$conf.int[,"lower .95"], 2) HR.confint.upper <- signif(x$conf.int[,"upper .95"],2) HR <- paste0(HR, " (", HR.confint.lower, "-", HR.confint.upper, ")") res<-c(beta, HR, wald.test, p.value) names(res)<-c("beta", "HR (95% CI for HR)", "wald.test", "p.value") return(res) #return(exp(cbind(coef(x),confint(x)))) }) res <- t(as.data.frame(univ_results, check.names = FALSE)) as.data.frame(res)

beta HR (95% CI for HR) wald.test p.value
age       0.019            1 (1-1)       4.1   0.042
sex       -0.53   0.59 (0.42-0.82)        10  0.0015
ph.karno -0.016      0.98 (0.97-1)       7.9   0.005
ph.ecog    0.48        1.6 (1.3-2)        18 2.7e-05
wt.loss  0.0013         1 (0.99-1)      0.05    0.83

The output above shows the regression beta coefficients, the effect sizes (given as hazard ratios) and statistical significance for each of the variables in relation to overall survival. Each factor is assessed through separate univariate Cox regressions.
From the output above,
The variables sex, age and ph.ecog have highly statistically significant coefficients, while the coefficient for ph.karno is not significant.
age and ph.ecog have positive beta coefficients, while sex has a negative coefficient. Thus, older age and higher ph.ecog are associated with poorer survival, whereas being female (sex=2) is associated with better survival.

Cox model, they want to estimate if a treatment is useful? 

什么是recursion, 什么时候能用它？

 https://www.dovov.com/recursion-7.html